はじめに

前回の記事ではRustでWAVファイルを扱う方法を調査しました.

今回はもう少し踏み込んで, フーリエ級数展開による波形の近似を行います.

フーリエ級数展開とは

フーリエ級数展開とは, ざっくり言えば任意の周期関数を三角関数の和で表現することです. これの何が嬉しいのかというと, 信号を時間の関数と考えることで信号を三角関数で近似したり, 周波数成分を抽出したりすることができます.

周期$T_0$の周期関数$f(t)$をフーリエ級数展開すると以下のような三角関数で表現できます.

$$f(t) = a_0 + \sum_{k=1}^{\infty} \left( a_k \cos \frac{2 \pi k}{T_0}t + b_k \sin \frac{2 \pi k}{T_0}t \right)$$

ここで, $a_0, a_k, b_k$はフーリエ係数と呼ばれます. $a_0$は直流成分つまりオフセットです. $a_k, b_k$はれぞれの周波数成分の振幅を表します.

導出は省きますが, フーリエ係数は以下の式で与えられます.

$$\begin{aligned} a_0 &= \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} f(t) dt\\\\ a_k &= \frac{2}{T_0} \int_{-T_0/2}^{T_0/2} f(t) \cos \left( \frac{2 \pi k}{T_0}t \right) dt\\\\ b_k &= \frac{2}{T_0} \int_{-T_0/2}^{T_0/2} f(t) \sin \left( \frac{2 \pi k}{T_0}t \right) dt \end{aligned}$$

矩形波の近似

以下のような矩形波をフーリエ級数展開を用いて近似してみます.

$$f(t) = \begin{cases} 1 & \left( 0 \leq t \leq \frac{T_0}{2} \right)\\\\ -1 & \left( -\frac{T_0}{2} \leq t \leq 0 \right) \end{cases}$$

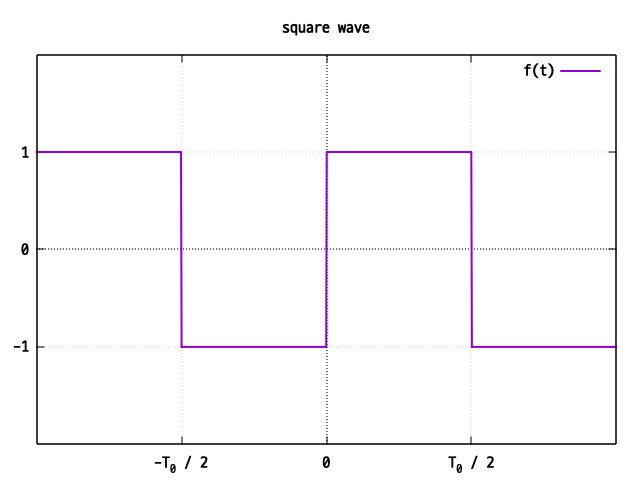
矩形波のフーリエ級数展開

与えられた矩形波は奇関数なので $a_0 = a_k = 0$ です. したがって $b_k$ のみを計算すれば良いことになります.

$$\begin{aligned} b_k &= \frac{2}{T_0} \int_{-T_0/2}^{T_0/2} f(t) \sin \left( \frac{2 \pi k}{T_0}t \right) dt \\\\ &= \frac{2}{T_0} \left\{ \int_{-T_0/2}^{0} (-1) \sin \left( \frac{2 \pi k}{T_0}t \right) dt + \int_{0}^{T_0/2} \sin \left( \frac{2 \pi k}{T_0}t \right) dt \right\} \\\\ &= \frac{2}{T_0} \left\{ \left[ \frac{T_0}{2 \pi k} \cos \left( \frac{2 \pi k}{T_0}t \right) \right]_{-T_0/2}^{0} - \left[ \frac{T_0}{2 \pi k} \cos \left( \frac{2 \pi k}{T_0}t \right) \right]_{0}^{T_0/2} \right\} \\\\ &= \frac{2}{\pi k} \left( 1 - \cos \pi k \right) \end{aligned}$$

ここで

$$\cos \pi k = \begin{cases} 1 & kが偶数のとき\\\\ -1 & kが奇数のとき \end{cases}$$

なので,

$$b_k = \begin{cases} 0 & kが偶数のとき\\\\ \frac{4}{\pi k} & kが奇数のとき \end{cases}$$

となります.

よって矩形波$f(t)$のフーリエ級数展開は以下のようになります.

$$f(t) = \sum_{k=1}^{\infty} \frac{4}{\pi (2k-1)} \sin \frac{2 \pi (2k-1)}{T_0}t$$

近似した波形の生成

フーリエ級数展開による矩形波の近似をグラフにしてみます. 今回は $\frac {1}{T_0} = 1[Hz]$ としています. Rustによる実装は以下の通りです.

今回はRustで実装していますが, フーリエ級数展開ができていればExcelでもグラフは描けます.

use std::f32::consts::PI;
use std::fs::File;
use std::io::{LineWriter, Write};

// 定数の定義
const SAMPLE_RATE: u32 = 8800;
const AMPLITUDE: f32 = 2.0;
const DUTY_CYCLE: f32 = 0.5;
const FREQUENCY: f32 = 1.0;
const OFFSET: f32 = -AMPLITUDE / 2.0;
const DURATION: f32 = 2.0 / FREQUENCY;

// 矩形波を生成する関数
fn generate_square_wave(
    num_samples: usize,
    frequency: f32,
    amplitude: f32,
    duty_cycle: f32,
) -> Vec<f32> {
    let period = 1.0 / frequency;
    let high_phase_duration = duty_cycle * period;

    (0..num_samples)
        .map(|n| {
            let time = n as f32 / SAMPLE_RATE as f32;
            let phase = time % period;
            let wave_amplitude = if phase < high_phase_duration {
                amplitude
            } else {
                0.0
            };
            wave_amplitude + OFFSET
        })
        .collect()
}

// 矩形波の近似をフーリエ級数展開の結果から生成する関数
fn generate_square_wave_approximation(num_samples: usize, frequency: f32, term: usize) -> Vec<f32> {
    (0..num_samples)
        .map(|n| {
            let time = n as f32 / SAMPLE_RATE as f32;
            let mut value = 0.0;

            for k in (1..=term).step_by(2) {
                value += 4.0 / (PI * k as f32) * (2.0 * PI * k as f32 * frequency * time).sin();
            }
            value
        })
        .collect()
}

fn main() {
    // サンプルの準備
    let num_samples = (DURATION * SAMPLE_RATE as f32) as usize;
    let square_wave = generate_square_wave(num_samples, FREQUENCY, AMPLITUDE, DUTY_CYCLE);
    let approximation_k1 = generate_square_wave_approximation(num_samples, FREQUENCY, 1);
    let approximation_k10 = generate_square_wave_approximation(num_samples, FREQUENCY, 10);
    let approximation_k100 = generate_square_wave_approximation(num_samples, FREQUENCY, 100);

    // ファイルに書き出し
    let file = File::create("output.dat").unwrap();
    let mut file = LineWriter::new(file);

    for n in 0..num_samples {
        let time = n as f32 / SAMPLE_RATE as f32;
        file.write_fmt(format_args!(
            "{} {} {} {} {}\n",
            time, square_wave[n], approximation_k1[n], approximation_k10[n], approximation_k100[n]
        ))
        .unwrap();
    }
}

実行すると以下のようなデータが出力されます. 左のカラムから順に時間(sec), 元の矩形波, $k=1$のときの近似, $k=10$のときの近似, $k=100$のときの近似です.

0 1 0 0 0
0.000113636364 1 0.0009090908 0.004545442 0.045441672
0.00022727273 1 0.0018181811 0.009090807 0.09080617
0.0003409091 1 0.0027272708 0.013636019 0.13601658
# --snip--

これをgnuplotでグラフにしてみます.

set term qt font "D2CodingLigature Nerd Font Mono, 12" size 600, 900

# ファイルの読み込みと最大値・最小値の計算
stats "output.dat" using 2 nooutput
max_value = STATS_max + 1
min_value = STATS_min - 1

# マルチプロットの設定
set multiplot layout 4, 1 title "Square Wave and Fourier Approximation"

set xlabel "Time (seconds)"
set ylabel "Amplitude"
set grid
set ytics 1
set xtics 0.5
set yrange [min_value:max_value]

# 矩形波のプロット
plot "output.dat" using 1:2 with lines title "Square Wave"

# 近似波のプロット(k=1)
plot "output.dat" using 1:3 with lines title "Approximation(k=1)"

# 近似波のプロット(k=10)
plot "output.dat" using 1:4 with lines title "Approximation(k=10)"

# 近似波のプロット(k=100)
plot "output.dat" using 1:5 with lines title "Approximation(k=100)"

unset multiplot

# 表示のために一時停止（必要に応じてコメントアウト）
pause -1

以下が出力結果です.

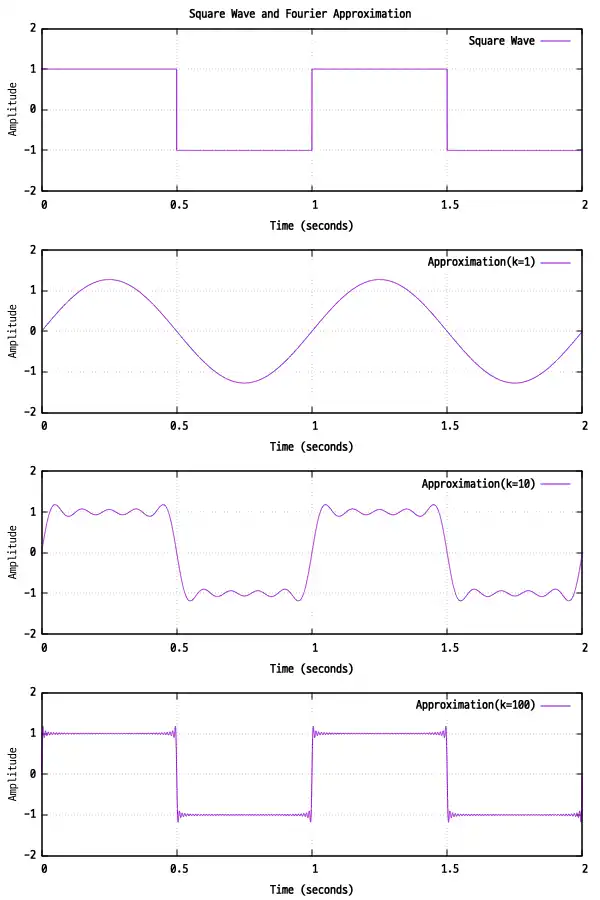
$k$の値が大きくなるほど元の矩形波に近づいていることがわかります.

おわりに

今回はフーリエ級数展開を用いて矩形波を近似してみました. Rustというよりは工業数学の話にはなってしまいましたが, 離散フーリエ変換(DFT)を実装する上でフーリエ級数展開は欠かせないので, 今回の記事はその前段階としての位置づけです.

次回はDFTを実装してみたいと思います.

参考文献

• 東北大学 やる夫で学ぶディジタル信号処理
• 東北大学 工業数学Ⅱ